Exploring the Randomness of LLMs
Large Language Models (LLMs) have become central to modern development—powering everything from RAG systems to AI agents that assist with our daily tasks.
Yet, most developers who rely on LLMs rarely pause to explore their behavior. Instead, they depend on benchmarks, anecdotal usage, or viral posts on X to form their mental models of what LLMs can (or cannot) do.
I believe this is risky—it creates a gap between people who use these models and those who deeply evaluate them. To help bridge that gap, I decided to run a simple but fun experiment:
Can LLMs Generate Random Numbers?
At first glance, this seems trivial. We know that LLMs cannot produce true randomness—they don’t have an internal random number generator. But the real questions are:
👉 Do LLMs show bias toward certain numbers when asked to generate a random one?
👉 Does this bias change across different models or families of models?
That’s what I set out to explore.
Experiment Setup
I designed a small test program to measure four things:
- The range of values generated when asked for random numbers
- The bias compared to a uniform random distribution
- The consistency of results across trials
- How results vary across different models and families
Prompts used:
prompts = {
"direct": f"Generate a random number between {min_val} and {max_val}. Return only the number, no explanation.",
"creative": f"Imagine you're a random number generator. Pick any number between {min_val} and {max_val}. Just return the number.",
"precise": f"Please provide exactly one number that falls within the range [{min_val}, {max_val}]. Return only the numeric value.",
}
Experiment parameters:
Number of trials = 5
Temperature = 0.7
Number ranges tested:
- [-1, 1]
- [-10, 10]
- [-100, 0]
- [0, 1]
- [0, 100]
- [1, 10]
- [1, 100]
Models tested:
- GPT-4.1
- GPT-4.1 Mini
- Claude 3.5 Haiku
- Claude 4 Sonnet
Total Cost:
- OpenAI API Cost = $5
- Claude API Cost = $5
Results
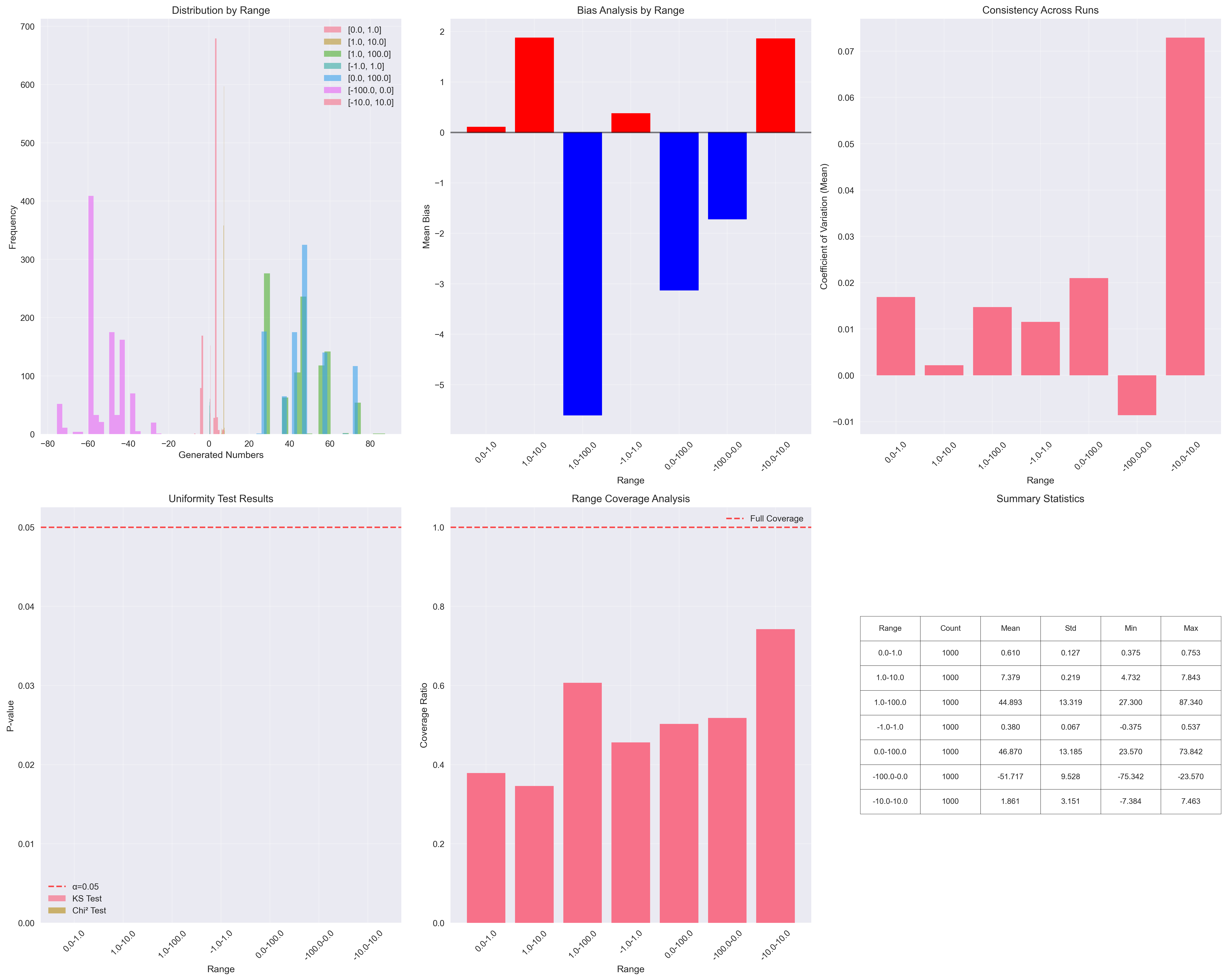
GPT-4.1 Mini
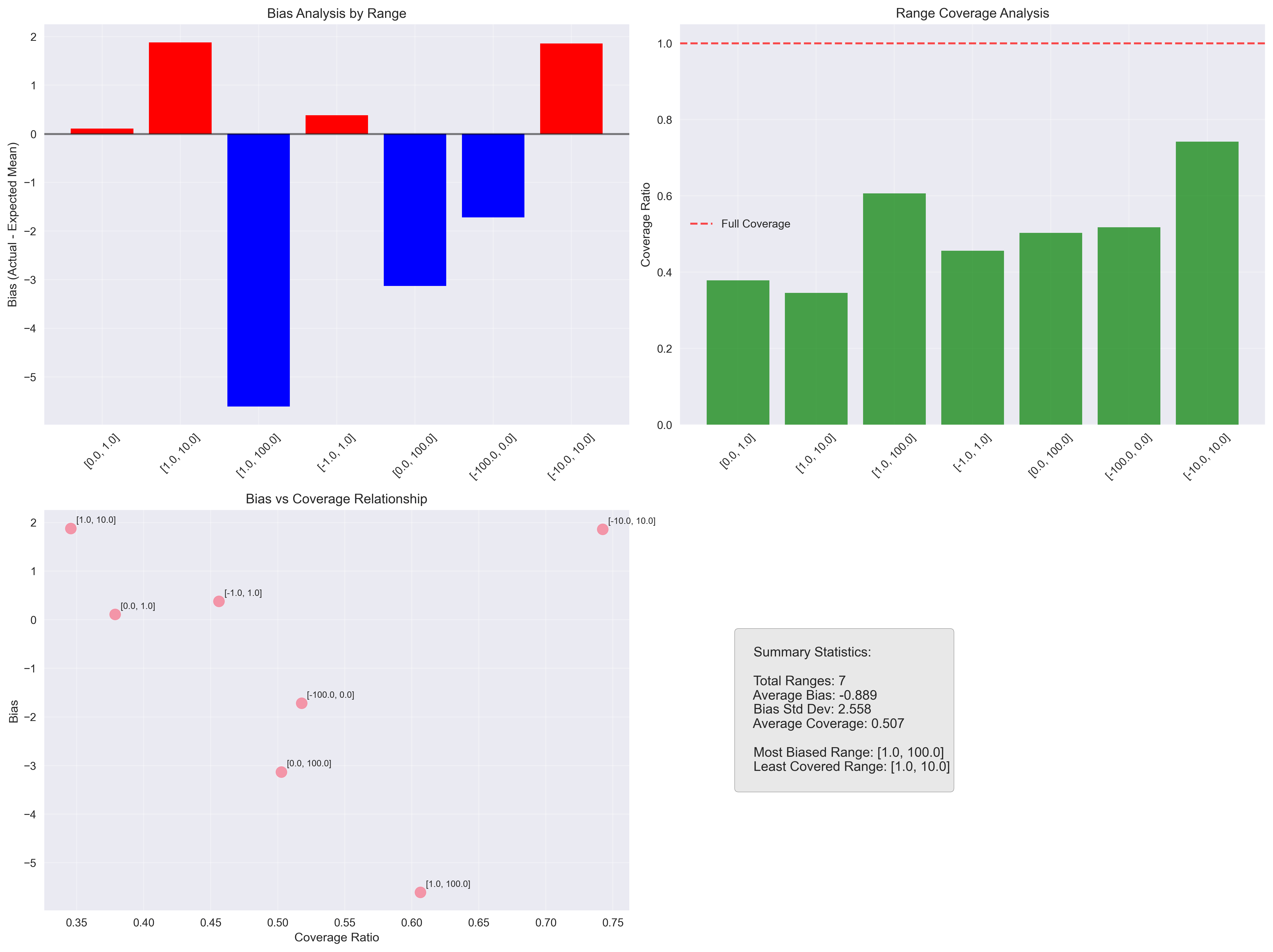
GPT-4.1
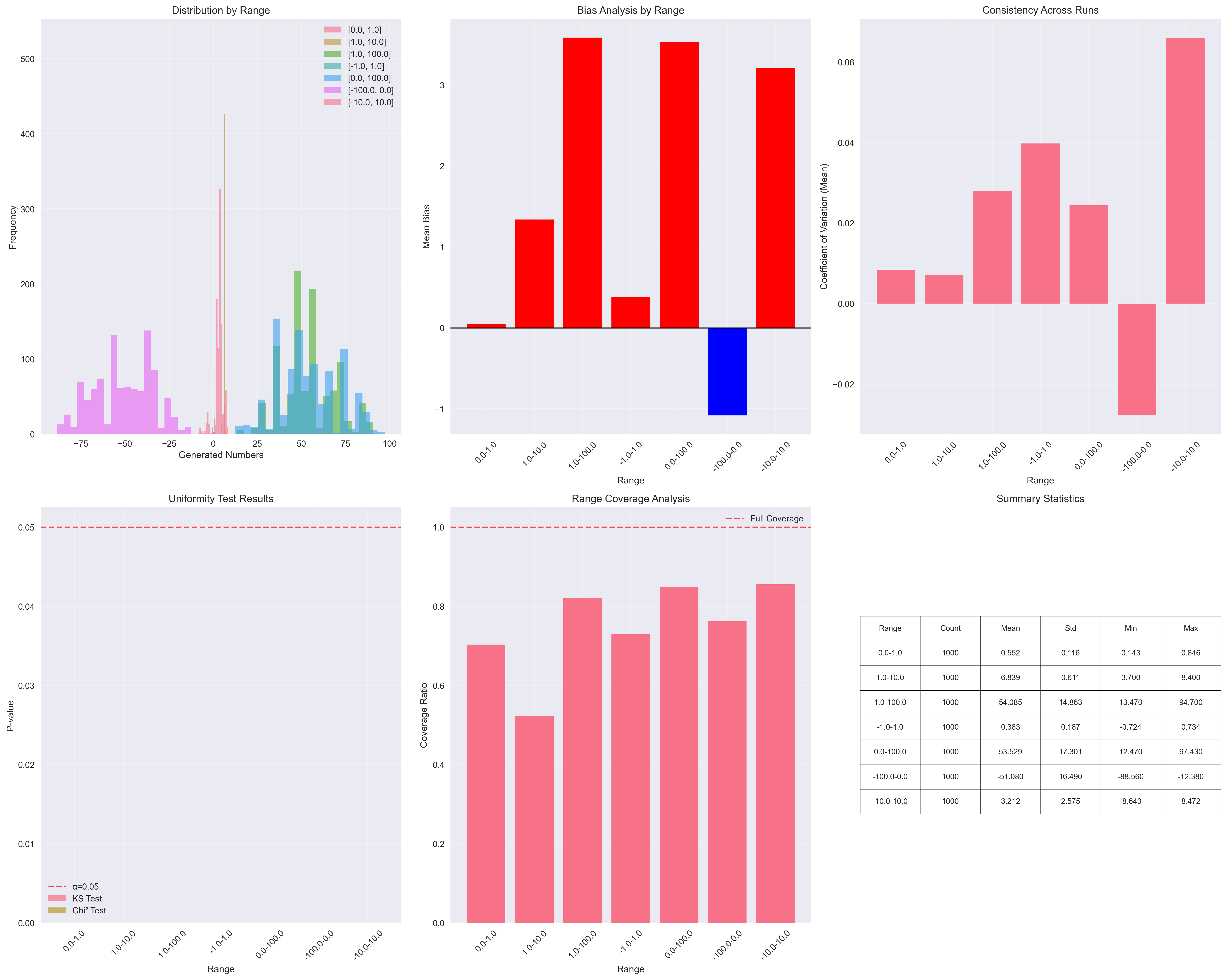
Claude 3.5 Haiku
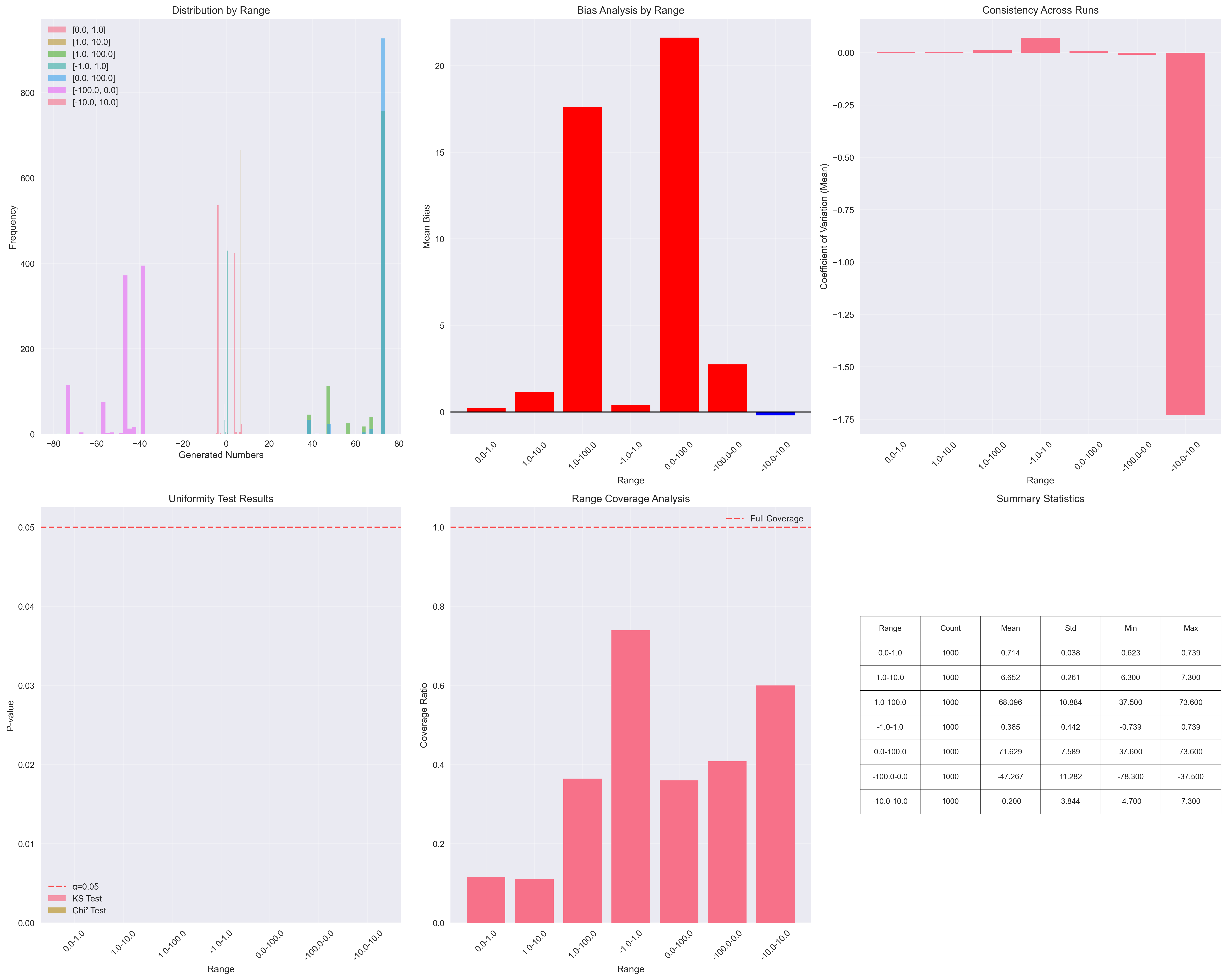
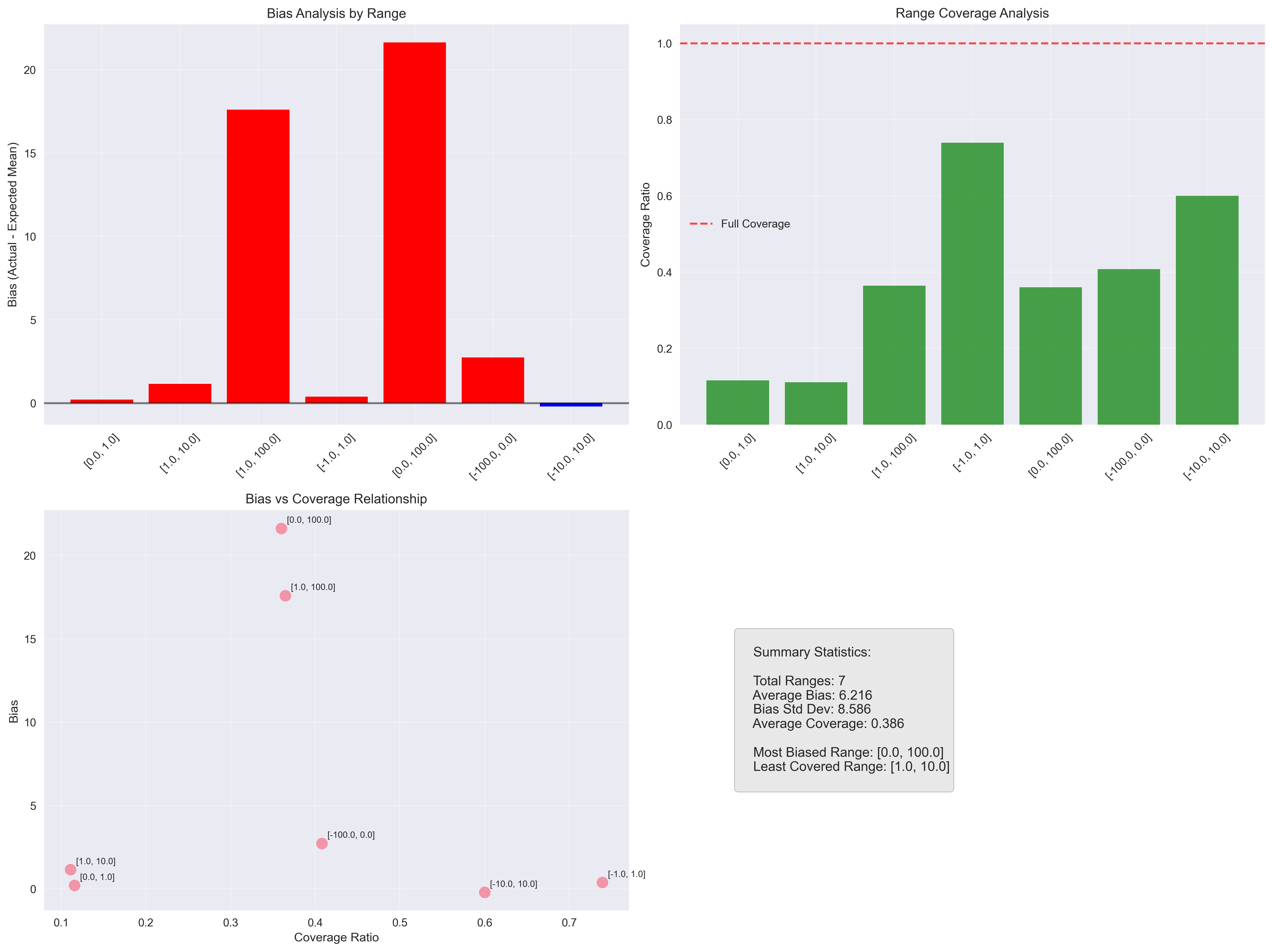
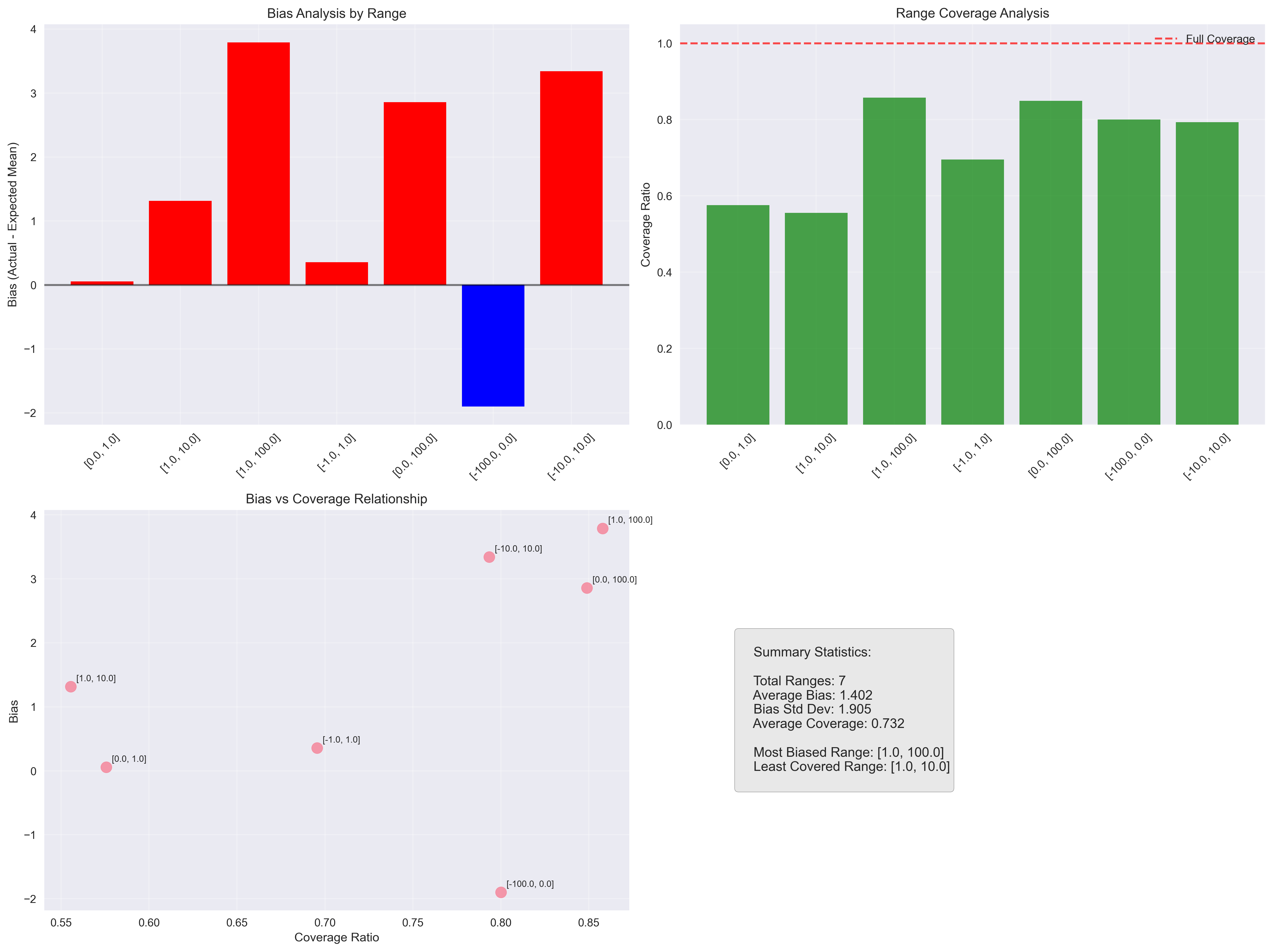
Claude 3.7 Sonnet
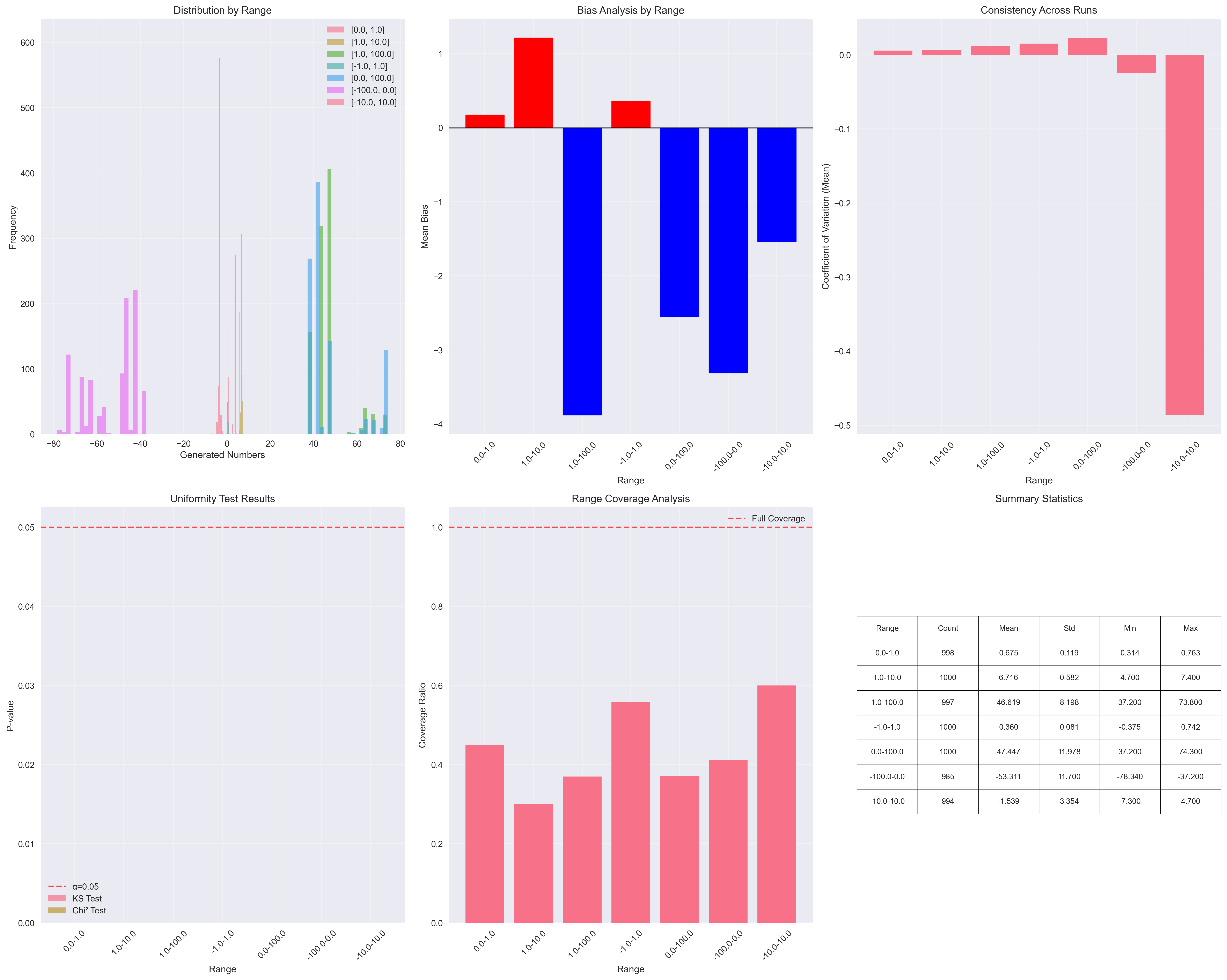
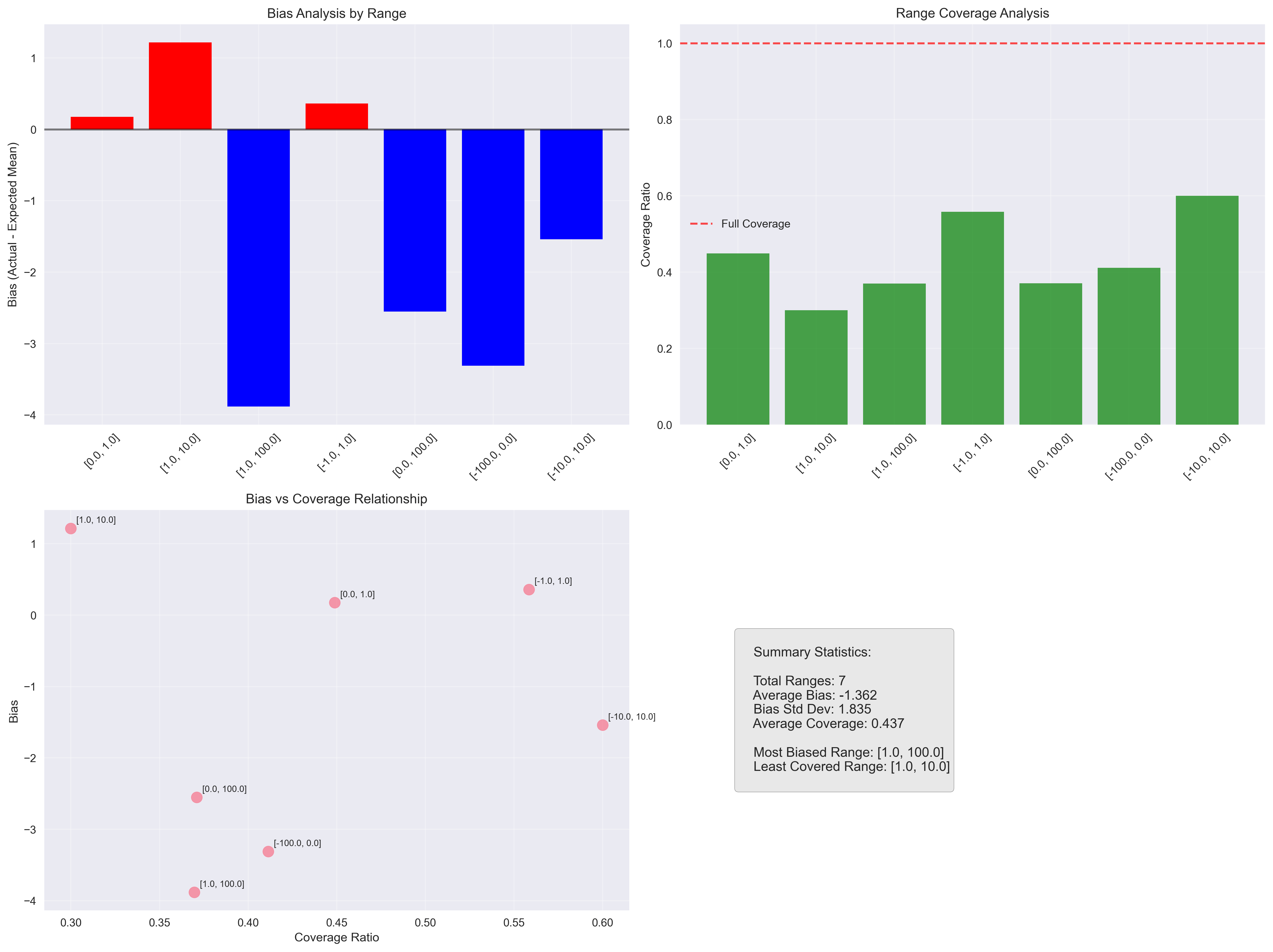
Learnings
This is just the beginning—but even from these early experiments, some clear patterns emerge.
The most surprising finding was how narrow the coverage of the total range was. Even in the best case, the models covered less than 90% of the possible values.
Another interesting point: larger models appear to be more consistent across different input ranges, as seen in the convergence graphs. This suggests that bigger models not only provide more stable answers but also maintain consistent behavior despite prompt variations.
